构建简单图形
我们知道可以使用Instantiate在场景中创建一个物品,那么我们可以通过for循环创建多个物品,通过改变不同物品的x和y轴,就可以呈现出不同的视觉效果。如下面的代码,会出现一条直线。
namespace DYFramework.Examples
{
public class Graph : MonoBehaviour
{
// 假设这时一个立方体预制体
[SerializeField] private Transform pointPrefab;
private void Start()
{
for (int i = 0; i < 10; i++)
{
Transform go = Instantiate(pointPrefab);
go.localPosition = new Vector3(i, 0, 0);
}
}
}
}从上面的代码可以看出立方体的坐标时从(0,0,0)~(10,0,0),因为y轴和z轴都为0,我们不妨将其省略掉,那么x的坐标范围为0~10
因为立方体的坐标按照中心点计算的,且立方体的大小为1×1×1,所以说视觉效果的范围其实为-0.5~10.5。在数学的角度来看,这就是函数的定义域,我们如何将函数的定义域限制在-1~1呢?
答案是缩小立方体的大小和改变立方体的x坐标。
我们来计算一下立方体的大小,要想限制在-1~1,它的长度为2。假设长度为2的线段中有count个立方体,那么一个立方体占用 2/count 的长度。那他们的坐标呢?因为坐标是按照中心点计算的,所以立方体的坐标为 (-1 + 2/count/2) ~ (1-2/count/2)
public class Graph : MonoBehaviour
{
[SerializeField] private Transform pointPrefab;
private void Start()
{
float count = 10;
for (float i = -1+ 2/count/2; i <= 1 - 2/count/2; i+=2/count)
{
Transform go = Instantiate(pointPrefab, transform,false);
go.localScale = Vector3.one * (2/count);
go.localPosition = new Vector3(i, 0, 0);
}
}
}为此我们可以封装为一个方法,其中xLeft和xRight为x的范围,count表示会生成多少个立方体。
namespace DYFramework.Examples
{
public class Graph : MonoBehaviour
{
[SerializeField] private Transform pointPrefab;
private void Start()
{
DrawCube(-1, 1, 10);
}
public void DrawCube(float xLeft, float xRight, int count)
{
float length = xRight - xLeft;
for (float i = xLeft+ length/count/2; i <= xRight - length/count/2; i+=length/count)
{
Transform go = Instantiate(pointPrefab, transform,false);
go.localScale = Vector3.one * (length/count);
go.localPosition = new Vector3(i, 0, 0);
}
}
}
}但是这种方法只会画一条直线,能不能画曲线。比如画一条 y = x^2。显然我们可以在代码中直接改变位置的y轴即可
public void DrawCube(float xLeft, float xRight, int count)
{
float length = xRight - xLeft;
var position = Vector3.zero;
for (float i = xLeft+ length/count/2; i <= xRight - length/count/2; i+=length/count)
{
Transform go = Instantiate(pointPrefab, transform, false);
go.localScale = Vector3.one * (length/count);
position.x = i;
position.y = i * i;
go.localPosition = position;
}
}如果只是单一的颜色,未免有点单调,我们可以为其添加一个shader。
我们可以使用URP通用渲染管线,如果你没有用过URP的话或者你创建的2D项目不是URP的话,可以在包管理工具中下载,下载完成后,如下图这种效果
但这不会自动使 Unity 使用 URP。我们首先必须通过 Assets / Create / Rendering / Universal Render Pipeline / Pipeline Asset (Forward Renderer) 为它创建一个资产。
然后接下来,转到项目设置 Graphics 部分并将创建的 URP 资产分配给该 Scriptable Renderer Pipeline Settings 字段。

我们可以创建一个ShaderGraph,如果你没有Shader Graph,同样的道理,你可以在包管理器中的搜索栏中搜索Shader Graph,然后直接下载。
创建一个新的 Shader Graph via Assets / Create / Shader / Universal Render Pipeline / Lit Shader Graph 并将其命名为 Point URP 。
Lit和UnLit是什么意思?
Lit是有光照,UnLit是无光照效果
可以通过在项目窗口中双击其资源或按其检查器中的 Open Shader Editor 按钮来打开图形。
这将为其打开一个 Shader Graph 窗口,该窗口可能会被多个节点和面板弄乱。
这些面板是 Blackboard、Graph Inspector 和主预览面板,它们可以调整大小,也可以通过工具栏按钮隐藏。还有两个链接节点:一个 Vertex 节点和一个 Fragment 节点。这两个选项用于配置 shader graph 的输出。
Shader Graph 由表示数据和节点组成。目前, Smoothness Fragment 节点的值设置为 0.5。要使其成为可配置的着色器属性,请按 Point URP 面板上的加号按钮,选择 Float ,然后将新条目命名为 Smoothness。这会向Blackboard添加一个表示属性的圆角按钮。选择它,然后将图形检查器切换到其 Node Settings 选项卡以查看此属性的配置。
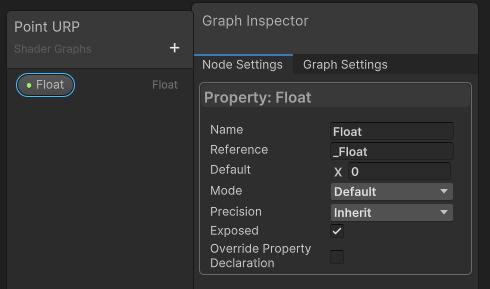
Reference 是内部已知属性的名称。然后将其下方的默认值设置为 0.5。确保启用其 Exposed 切换选项,因为这会控制材质是否为其获取着色器属性。最后,要使其显示为滑块,请将其 Mode 更改为 Slider 。
接下来,将圆角 Smoothness 按钮从黑板拖动到图表中的空白区域。这将向图表中添加一个 smoothness 节点。通过从其中一个点拖动到另一个点,将其连接到 PRB Master 节点的 Smoothness 输入。这将在它们之间建立联系。
现在,您可以通过 Save Asset 工具栏按钮保存图表,并创建一个使用它的材质 Point URP 。着色器的菜单项为 Shader Graphs / Point URP 。然后使 Point 预制件使用该材质。
要为点着色,我们必须从 position 节点开始。通过在图形的空白部分打开上下文菜单并从 New Node 中进行选择来创建一个。选择 Input / Geometry / Position 或仅搜索 Position 。
使用相同的方法创建 a Multiply 和 an Add 节点。使用这些选项可将位置的 XY 分量缩放 0.5,然后添加 0.5,同时将 Z 设置为零。这些节点根据它们所连接的内容调整其输入类型。因此,首先连接节点,然后填写它们的常量输入。然后将结果连接到 Fragment 的 Base Color 输入。
如果将鼠标悬停在 Multiply 和 Add 节点上,则可以通过按其右上角显示的箭头来压缩这些节点的视觉大小。这将隐藏所有未连接到花药节点的输入和输出。这消除了很多杂乱。您还可以通过 Vertex 和 Fragment 节点的上下文菜单删除其组件。这样,您可以隐藏保持其默认值的所有内容。
保存着色器资源后,我们现在在播放模式下获得与使用默认渲染管道时相同的彩色点。除此之外,调试更新程序还会显示在播放模式下的单独 DontDestroyOnLoad 场景中。这是用于调试 URP 的,可以忽略。
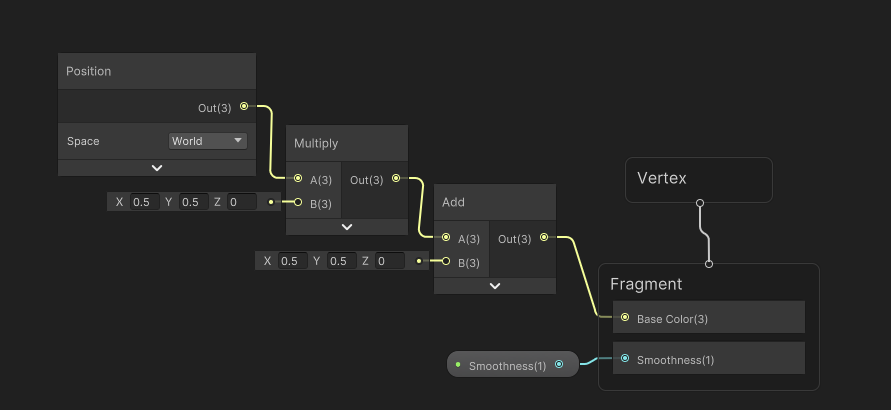
然后运行项目,就可以看到立方体的颜色会随着立方体世界位置不同而发生改变
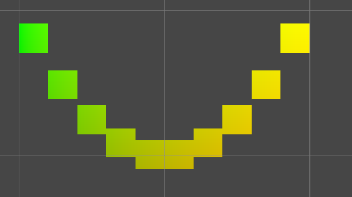
但是图形无法动起来啊!要想动起来也比较简单,我们只需要拿到所创建的立方体,然后在Update改变其y轴的位置就可以让其动起来。
在此之前,我们先去设置一个正弦波的函数。
namespace DYFramework.Examples
{
public class Graph : MonoBehaviour
{
[SerializeField] private Transform pointPrefab;
private List<Transform> _transforms = new();
private void Start()
{
DrawSinFun(-1, 1, 50);
}
public void DrawSinFun(float xLeft, float xRight, int count)
{
float length = xRight - xLeft;
var position = Vector3.zero;
for (float i = xLeft+ length/count/2; i <= xRight - length/count/2; i+=length/count)
{
Transform go = Instantiate(pointPrefab, transform,false);
go.localScale = Vector3.one * (length/count);
position.x = i;
position.y = Mathf.Sin(i * Mathf.PI);
go.localPosition = position;
_transforms.Add(go);
}
}
}
}
效果如下:
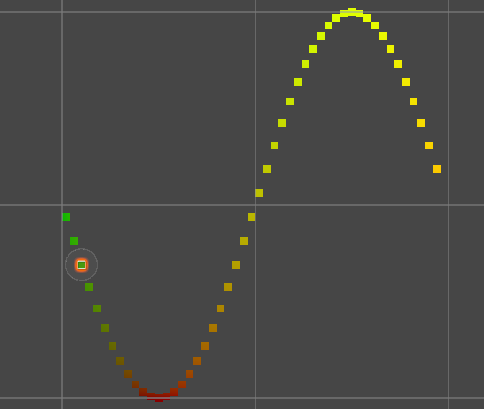
接下来我们可以让其动起来
要为该函数设置动画,请在计算 sin 函数之前将当前游戏时间添加到 X。它是通过 Time.time .如果我们将时间也缩放 π,该函数将每两秒重复一次。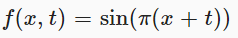
整体代码如下,为了让视觉效果更好,我重新设置了输入的参数
using System;
using System.Collections.Generic;
using UnityEngine;
namespace DYFramework.Examples
{
public class Graph : MonoBehaviour
{
[SerializeField] private Transform pointPrefab;
private List<Transform> _transforms = new();
private void Start()
{
DrawSinFun(-5, 5, 100);
}
public void DrawSinFun(float xLeft, float xRight, int count)
{
float length = xRight - xLeft;
var position = Vector3.zero;
for (float i = xLeft+ length/count/2; i <= xRight - length/count/2; i+=length/count)
{
Transform go = Instantiate(pointPrefab, transform,false);
go.localScale = Vector3.one * (length/count);
position.x = i;
position.y = Mathf.Sin(i * Mathf.PI);
go.localPosition = position;
_transforms.Add(go);
}
}
private void Update()
{
float time = Time.time;
for (var i = 0; i < _transforms.Count; i++)
{
Transform point = _transforms[i];
Vector3 pos = point.localPosition;
pos.y = Mathf.Sin(Mathf.PI * (pos.x + time));
point.localPosition = pos;
}
}
}
}


评论区